MOMENT OF STATICAL STABILITY FORMULA : EXAMPLE SHIP STABILITY CALCULATIONS

MOMENT OF STATICAL STABILITY FORMULA : EXAMPLE SHIP STABILITY CALCULATIONS

When a ship is inclined by an external force, such as wind and wave action, the centre of buoyancy moves out to the low side, parallel to the shift of the centre of gravity of the immersed and emerged wedges, to the new centre of gravity of the under-water volume.

The force of buoyancy is considered to act vertically upwards through the centre of buoyancy.The weight of the ship is considered to act vertically downwards through the centre of gravity.

These two equal and opposite forces produce a moment or couple which may tend to right or capsize the ship.
The moment is referred to as the moment of statical stability and may be defined as the moment to return the ship to the initial position when inclined by an external force.

A ship which has been inclined by an external force is shown in picture below .The centre of buoyancy has moved from B to B1 parallel to gg1, and the force of buoyancy (W) acts vertically upwards through B1. The weight of the ship (W) acts vertically downwards through the centre of gravity (G).

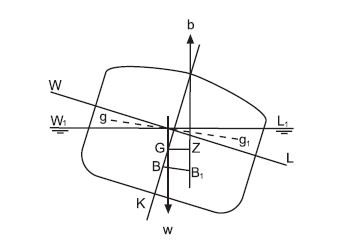
The perpendicular distance between the lines of action of the forces (GZ) is called the righting lever. Taking moments about the centre of gravity, the moment of statical stability is equal to the product of the righting lever and
the displacement, or:

Moment of statical stability=W x GZ

THE MOMENT OF STATICAL STABILITY AT A SMALL ANGLE OF HEEL

At small angles of heel the force of buoyancy may be considered to act vertically upwards through a fixed point called the initial metacentre (M).This is shown in picture below, in which the ship is inclined to a small angle (Ꝋ degrees).

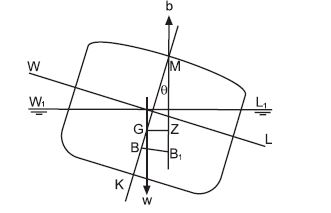
• Moment of statical stability =W x GZ
• But in triangle GZM: GZ=GM sinꝊ˚
• Moment of statical stability = W x GM x sinꝊ˚

From this formula it can be seen that for any particular displacement at small angles of heel, the righting moments will vary directly as the initial metacentric height (GM).

Hence, if the ship has a comparatively large GM she will tend to be `stiff’, whilst a small GM will tend to make her `tender’. It
should also be noticed, however, that the stability of a ship depends not only upon the size of the GM or GZ but also upon the displacement.

Thus two similar ships may have identical GM’s, but if one is at the light displacement and the other at the load displacement, their respective states of stability will be vastly different. The ship which is at the load displacement will be much more `stiff’ than the other.

EXAMPLE SHIP STABILITY CALCULATIONS

Example 1

A ship of 4000 tonnes displacement has KG 5.5m and KM 6.0 m. Calculate the
moment of statical stability when heeled 5 degrees.

GM=KM-KG=6.0-5.5=0.5m
Moment of statical stability = W x GM x sin Ꝋ˚=4000 x0.5 x sin 5˚
Moment of statical stability=174.4 tonnes m

Example 2

When a ship of 12 000 tonnes displacement is heeled 6 1/2 degrees the moment of statical stability is 600 tonnes m.
Calculate the initial metacentric height.

Moment of statical stability = W x GM x sin Ꝋ˚
GM = (moment of statical stability)/(W x sin⁡θ°)
= 600/(12000 x 6 1/2)
GM = 0.44 m

RELATED ARTICLE

TRANSVERSE STABILITY OF SHIP : SHIP STABILITY AND THE MOVEMENT OF CENTRE GRAVITY ‘G’

INSTRUCTIONS FOR THE GUIDANCE OF SURVEYORS ON DAMAGE STABILITY SOLAS 2020 AMENDMENTS